0.1 线性回归
使用直线拟合的方法得到拟合直线称之为线性回归(linear regression).如果只有一个自变量,则称之为简单线性回归(simple),有多个自变量,则称之为多元线性回归(multiple regression).这两个模型都必须满足变量是连续性变量,如果变量为分类变量,也可以进行线性回归,称之为逻辑回归(logistic regression).
0.1.1 简单线性回归
我们举个例子,年龄和身高是否有线性关系,是否可以使用年龄来预测身高呢?
age <- 18:29
height <-
c(76.1,77,78.1,78.2,78.8,79.7,79.9,81.1,81.2,81.8,82.8,83.5)
data <-
data.frame(age, height,
stringsAsFactors = FALSE)
library(ggplot2)
(
plot <-
ggplot(data, aes(age, height)) +
geom_point() +
theme_bw()
)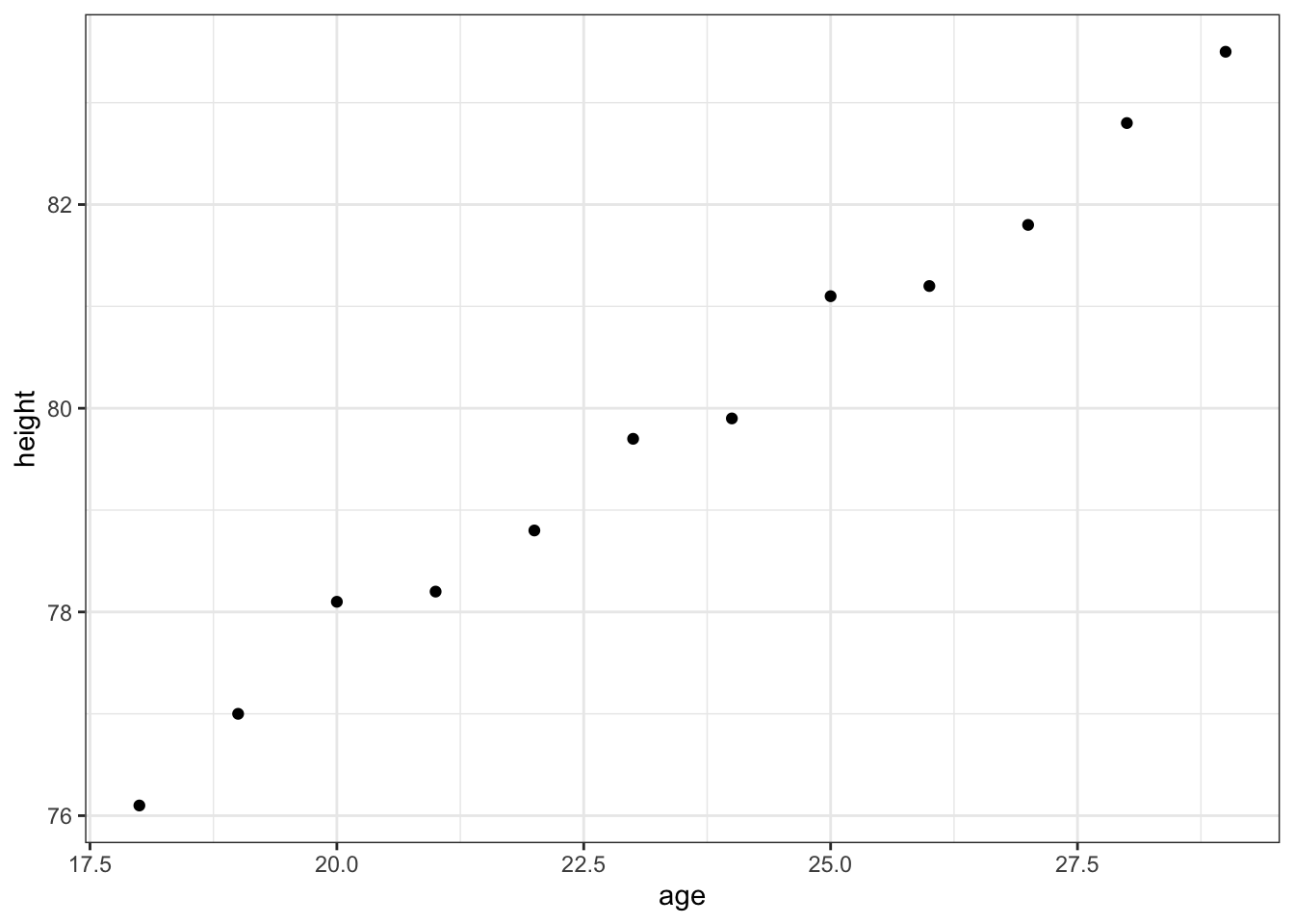
我们画出散点图之后,可以看出age和height呈比较明显的线性关系.
那我们怎么用一条直线去拟合(fit)数据呢?我们使用的就是最小平方差法(least square).
那么最简单的拟合办法是什么呢?也就是直接使用所有人的height的平均值去拟合.
plot +
geom_hline(yintercept = mean(data$height))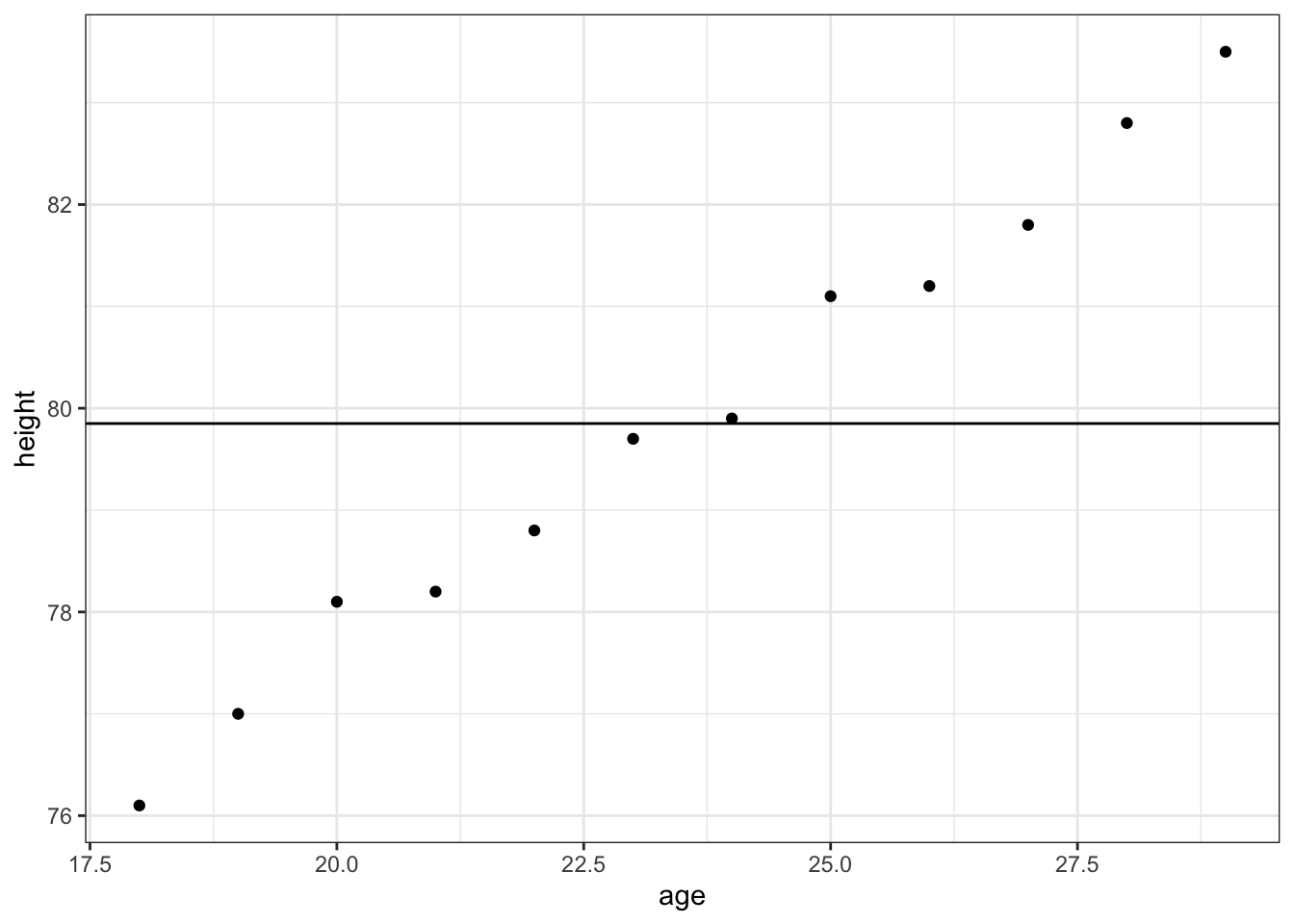
那么怎么评价一条直线对数据拟合的好坏呢?这时候就需要引入另外一个概念,残差(residuls).残差也就是真实值和拟合值之间差值:
\[residual = y_i - y_i^{'}\]
其中\(y_i\)是真实值,而\(y_i{'}\)是模型预测值.
plot +
geom_hline(yintercept = mean(data$height)) +
geom_segment(aes(x = data$age[1], y = data$height[1], xend = data$age[1], yend = mean(data$height)), colour = "red", arrow = arrow()) ## Warning: Use of `data$age` is discouraged. Use `age` instead.## Warning: Use of `data$height` is discouraged. Use `height` instead.## Warning: Use of `data$age` is discouraged. Use `age` instead.## Warning: Use of `data$height` is discouraged. Use `height` instead.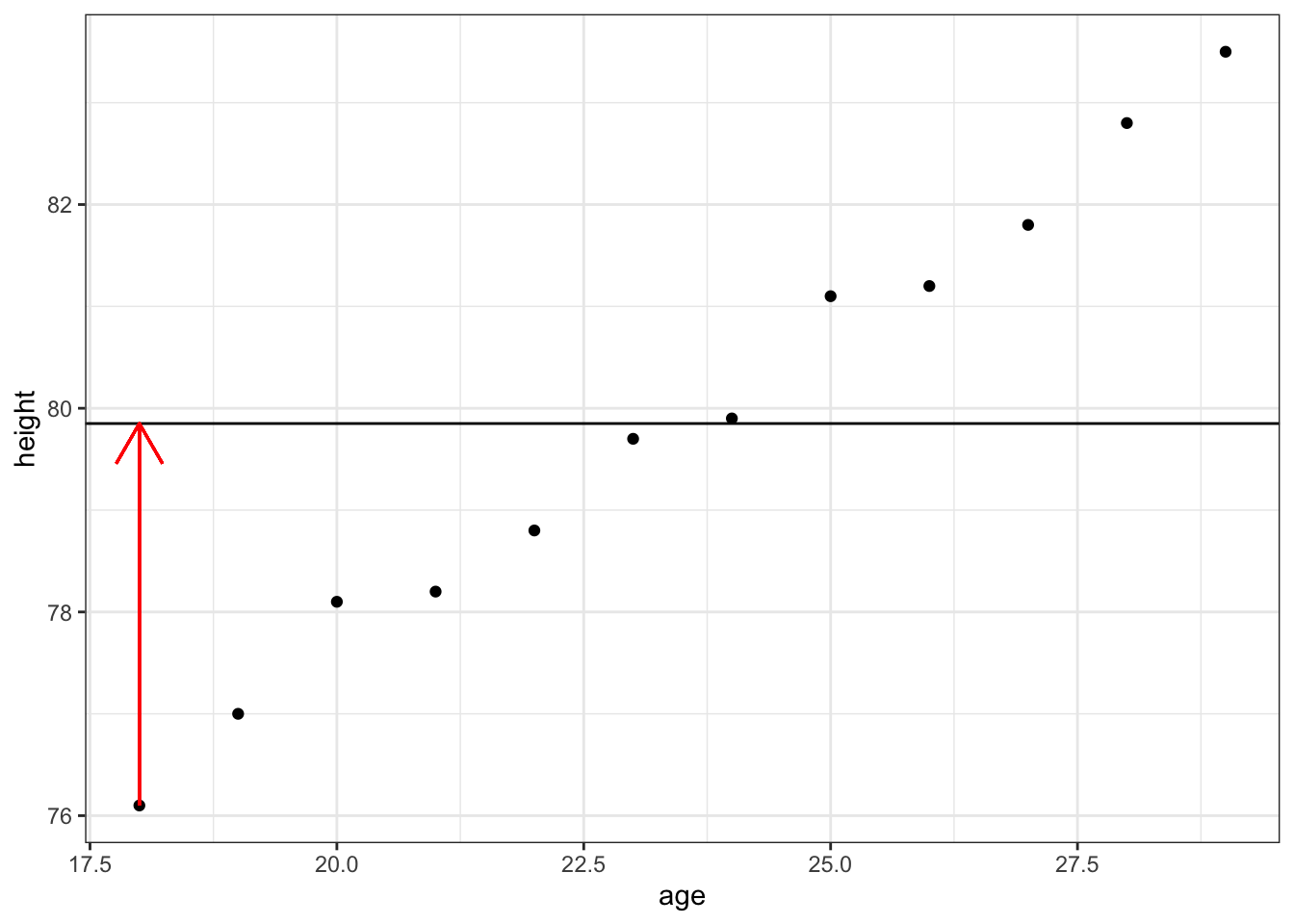
从定义可以看到,残差有正有负.为了表示一条拟合直线对数据拟合的程度的好坏,我们将残差平方然后加和,从而得到残差平方和(sum of squared residuals),该值就可以用来表示一条直线对数据的拟合的好坏.拟合的越好,该值越小,拟合的越差,该值越大.
其实使用残差平方和作为损失函数得到的最后的方程或者说模型并不一定是最优解,但是好处是方便后面求解(求导)并且解是唯一的.另外还有使用残差绝对值之和作为损失函数进行求解.以后再慢慢介绍.
\[sum \quad of \quad squared \quad residuals = \sum_{i=1}^n(y_i-y_i^{'})^2\]
注意,该值是有量纲的,只能比较同一组数据不同拟合直线的好坏,而不能比较不同数据之间的拟合的好坏.后面会介绍\(R^2\).
那么怎样找到一个最好的拟合直线呢?我们可以将这条线(平均值)进行旋转,每条直线都会有截距(intersect)和斜率(slope)两个参数,对于每一条直线,我们都会计算其残差平方和.
最后,我们会得到一系列的截距和斜率组合以及他们所对应的残差平方和.我们可以简单的理解,直接选取残差平方和最小的参数组合即可(实际情况更为复杂一些).从而得到最佳的参数组合.这也是为什么这种方法称之为’least square’的原因.
那么如何估量一个拟合直线的好坏呢?这时候就需要引入\(R^2\)的概念.
0.1.2 \(R^2\)
首先,我们计算使用身高平均值拟合直线的残差平方和,称之为\(SS(mean)\)
\[SS(mean) = (data - mean)^2\]
同时,我们知道方差(Var(mean))等于残差平方和除以样本个数:
\[Var(mean) = \frac{SS(mean)}{n}\]
然后,按照同样的方法,我们计算拟合直线的残差平方和,称之为\(SS(fit)\).同时,我们也可以计算出来拟合直线的方差(Var(fit)).
可以看到,拟合直线得到的残差平方和要比平均值得到的要小,也就是说,将年龄因素考虑进去之后,身高的方差有一部分能够被年龄所解释.
\(R^2\)告诉我们年龄可以解释多少比例的身高的方差.
\[R^2 = \frac{Var(mean) - Var(fit)}{Var(mean)} = \frac{SS(mean) - SS(fit)}{SS(mean)} = 1 - \frac{ SS(fit)}{SS(mean)}\]
从公式可以看出,如果一条直线正好穿过所有的数据点,那么\(SS(fit)=0\),这时候\(R^2=1\).而如果身高和年龄完全没有关系,则\(R^2 = 0\).
需要注意的是,\(R^2\)的大小并不具有统计学意义,我们可以想象,如果只有两个点,那么必定有一条直线通过他们,因此\(SS(fit)\)为0,但是很明显这样的fit是没有意义的,得到的\(R^2\)也并不能说明两个变量之间真是的关系.这说明了样本的数量也同样重要,因此,我们需要对\(R^2\)进行统计学假设检验,得到其统计学显著性,也就是p value.
0.1.3 \(R^2\)的假设检验
首先,我们需要明白\(R^2\)的含义,我们上面已经讨论过了,\(R^2\)指的是变量x能够解释变量y的方差的比例.比如上面的例子,\(R^2\)为0.99,说明年龄可以解释99%的身高的方差.
这时候,需要引入一个统计量,F:
\[F = \frac{(Var(mean) - Var(fit))/(p_{fit}-p_{mean})}{Var(fit)/(n-p_{fit})} = \frac{(SS(mean) - SS(fit))/(p_{fit}-p_{mean})}{SS(fit)/(n-p_{fit})} = \frac{\frac{(SS(mean) - SS(fit))}{p_{fit}-p_{mean}}} {\frac{SS(fit)}{n-p_{fit}}}\]
也就是说,F等于变量x能够解释变量y的方差除以变量x不能够解释变量y的方差.
而\((n-p_{fit})/(p_{fit}-p_{mean})\)则称之为自由度(degrees of freedoms).自由度的定义以后再详细解释.
其中\(p_{fit}\)代表回归方程中参数的数目,比如一元线性方程中,只有两个参数(intercept和slop),所以\(p_{fit}=2\).\(p_{mean}\)代表平均值直线的参数个数,在一元线性方程中,为1.n是数据集的样本个数.
因此,\(p_{fit}-p_{mean}\)代表的含义是该拟合模型与平均值模型相比,多出来的参数的个数.在简单线性回归中,多出来的就是slope.对于多元线性回归,比如,两个自变量预测一个因变量,则这时候\(p_{fit}=3\).
我们再来看分母,为什么需要使用\(SS(fit)\)除以\(n-p_{fit}\)呢?因为我们知道模型越复杂(参数越多),你就需要更多的点去拟合.比如,对于两个点的一元一次方程,只需要两个点即可(两点确定一条直线).而对于二元一次方程,则需要三个点去拟合.
这时候我们再来看分子分母分别代表什么意义.
分子:拟合模型多出来的参数能够解释的方差(变异).
分母:拟合模型多出来的参数不能够解释的方差(变异).
这样我们拿到F值以后,怎么计算p value呢?其实就是使用permutation test的方法.
随机产生与数据集样本数相同数目的数据集.
对其进行拟合并计算每一组随机数据的F值.
产生大量的随机F值,并得到随机F值的分布.
拿到随机F值的分布,p value就等于大于真实F值的数目除以随机F值的总数目.
当然,所有随机F值的分布其实是符合F分布的,拿到了F分布,就可以计算p value.F分布以后再详细介绍.
0.1.4 矫正\(R^2\)(\(adjusted R^2\))
什么是矫正\(R^2\)呢?我们从\(R^2\)定义可以看到,如果我们增加了拟合模型的变量个数,因为\(SS(mean)\)是固定的,因此\(SS(fit)\)都会减小,所以导致\(R^2\)变大,从而造成过拟合(over fitting).因此,我们需要对模型选入的变量个数做一个惩罚,这就是\(adjusted \quad R^2\).以后再详细解释.
0.1.5 系数的假设检验
同样的,我们可以看到,上面是对\(R^2\)做假设检验,当然我们也需要对每个变量的系数(包括intersect)进行假设验证,在多元回归中尤其重要,我们会在以后进行详细解释.
0.1.6 R语言进行线性回归
R语言中的lm()函数可以用来进行线性回归.使用方法如下:
lm_fit <-
lm(height ~ age, data)
summary(lm_fit)##
## Call:
## lm(formula = height ~ age, data = data)
##
## Residuals:
## Min 1Q Median 3Q Max
## -0.27238 -0.24248 -0.02762 0.16014 0.47238
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 64.9283 0.5084 127.71 < 2e-16 ***
## age 0.6350 0.0214 29.66 4.43e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 0.256 on 10 degrees of freedom
## Multiple R-squared: 0.9888, Adjusted R-squared: 0.9876
## F-statistic: 880 on 1 and 10 DF, p-value: 4.428e-11summary中提供了该线性回归的大部分内容.其中Multiple R-squared其实就是R-squared\(R^2\),而Adjusted R-Squred主要是对多元线性回归时对多个变量进行矫正,因为当变量数目增加的时候,\(R^2\)总会变小,因此需要对其进行矫正.对于简单线性回归来说.直接使用Multiple R-squared即可,而对于多元线性回归来说,则需要使用Adjusted R-Squred来衡量模型拟合的效果.